ガウス分布 (Gaussian distribution)¶
ガウス確率変数の変数変換¶
確率変数 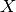 が平均
が平均 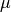 , 分散
, 分散 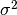 のガウス分布 に従い, 確率変数
のガウス分布 に従い, 確率変数 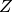 が平均 0, 分散 1 のガウス分布 に従うとする. これらの確率変数に関する期待値を
が平均 0, 分散 1 のガウス分布 に従うとする. これらの確率変数に関する期待値を
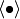 と書く. 統計量
と書く. 統計量 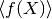 (
(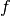 は適当な関数) は
は適当な関数) は 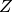 を用いて,
を用いて,
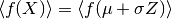
と計算出来る.
形式的な変数変換で示そう. 平均 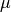 , 分散
, 分散 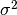 のガウス確率密度関数を
のガウス確率密度関数を
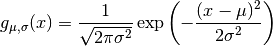
と書く. 変数変換 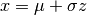 をすれば,
をすれば,
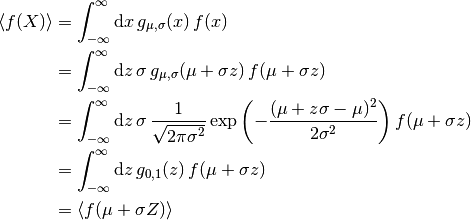
ガウス測度 (Gaussian measure)¶
物理の計算では, いくつものガウス積分が出てくることが多々あり, その度に
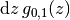 などと書くのは煩雑なので, ガウス測度
(Gaussian measure) と呼ばれる以下の記法を導入する.
などと書くのは煩雑なので, ガウス測度
(Gaussian measure) と呼ばれる以下の記法を導入する.
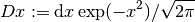
これを用いれば, ガウス確率変数の変数変換 の公式は
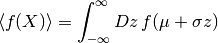
とかける.
注釈
ただの省略のための記法なので, 数学の測度論 (measure theory) とは深い関わりなど無いし, そもそも測度論の測度は集合をとる関数なので別物である
(測度論で似た記法を 別の 場面で使う流儀はあるが...). 物理の分野では
 と繰り返し書くのが面倒なので使われているだけである.
と繰り返し書くのが面倒なので使われているだけである.
Q関数¶
標準ガウス分布の裾 (tail) は Q関数 (Q-function) と呼ばれ, ガウス分布を取り扱う計算では頻出である.
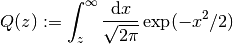
興奮・抑制均衡のオリジナルの論文 [vanVreeswijk1998] ではこのQ関数は
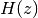 と表記され, 相補誤差関数
(complementary error function, erfc)
と呼ばれているが, 広く使われている定義
と表記され, 相補誤差関数
(complementary error function, erfc)
と呼ばれているが, 広く使われている定義
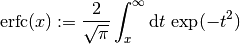
からは, 少し違う. erfc と Q関数 の間には,
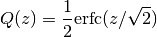
の関係がある.
ヘヴィサイド関数の多重ガウス積分とQ関数¶
ヘヴィサイド関数 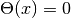 (
( ),
),
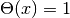 (
(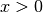 ), の多重ガウス積分とQ関数には次の関係が成り立つ.
), の多重ガウス積分とQ関数には次の関係が成り立つ.
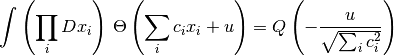
ただし, 積と和は 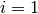 から
から 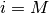 までについておこない,
積分区間は
までについておこない,
積分区間は 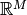 全体とする.
全体とする.
まずは 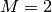 の場合について示す.
の場合について示す.
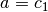 ,
, 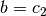 ,
, 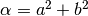 とする.
とする.
二次元ベクトル 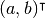 に沿った単位ベクトルを
に沿った単位ベクトルを 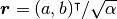 と定義する. [1] これに直交した2つある単位ベクトル
と定義する. [1] これに直交した2つある単位ベクトル
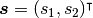 のうち, 行列式が
のうち, 行列式が 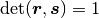 となるものを選ぶ.
[2]
となるものを選ぶ.
[2]
| [1] | 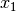 と と 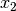 に関するガウス積分を に関するガウス積分を
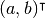 の軸に沿ったガウス積分とそれに直交する軸に沿ったガウス積分に分ける, というアイディアである. の軸に沿ったガウス積分とそれに直交する軸に沿ったガウス積分に分ける, というアイディアである. |
| [2] | 行列式が 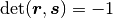 となるものを選んでも同様に計算できる. となるものを選んでも同様に計算できる. |
これらの仮定, つまり,
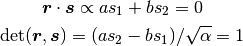
より, [3] 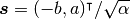
| [3] | 第一式より 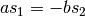 , 第二式の両辺に , 第二式の両辺に  をかけて
をかけて 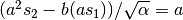 なので, なので,
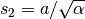 . 第一式より, . 第一式より,
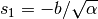 である. である. |
変数変換
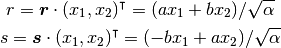
を施す. ヤコビアンは,
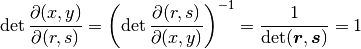
なので, 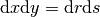 である. さらに,
である. さらに,
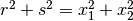 なので, 結局,
なので, 結局,
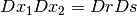 である.
である.
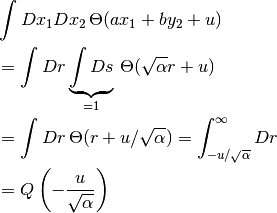
一般の 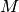 に関して成り立つことは, 帰納法で確かめられる.
に関して成り立つことは, 帰納法で確かめられる.