マスター方程式¶
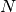 個の二状態をとるニューロン (binary neuron) が相互に作用している確率的な系を考える. ニューロン
個の二状態をとるニューロン (binary neuron) が相互に作用している確率的な系を考える. ニューロン 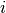 の状態は 0 または 1 をとる状態変数
の状態は 0 または 1 をとる状態変数 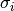 で表され, 系全体の状態はベクトル
で表され, 系全体の状態はベクトル
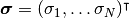 で表される
(つまり,
で表される
(つまり, 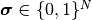 ). ここではこれらの状態変数の連続時間
). ここではこれらの状態変数の連続時間 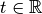 に沿った変化を考えるが, 時間に関する依存性を表記上は省略して
に沿った変化を考えるが, 時間に関する依存性を表記上は省略して 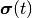 を
を 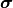 と書く.
と書く.
表記の準備をする.
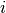 番目のニューロンの状態を反転した状態ベクトルを
番目のニューロンの状態を反転した状態ベクトルを
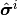 ,
, 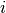 番目の成分を除いた状態ベクトルを
番目の成分を除いた状態ベクトルを 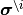 (つまり,
(つまり, 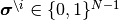 )
と書くことにする. 形式的にかけば,
)
と書くことにする. 形式的にかけば,
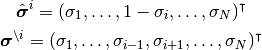
である. ニューロン 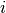 以外の状態
以外の状態 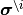 が与えられた時に, ニューロン
が与えられた時に, ニューロン 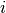 が状態を
が状態を 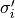 から
から
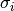 に遷移させる単位時間あたりの確率を
に遷移させる単位時間あたりの確率を
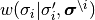 で表す.
つまり,
で表す.
つまり, 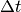 時間の間にこの遷移を起こす確率は,
時間の間にこの遷移を起こす確率は,
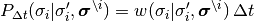
である. ここでは, 系が時間 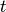 に 状態
に 状態 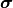 をとる確率
をとる確率
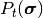 の時間発展が,
マスター方程式 (master equation) とよばれる次の微分方程式 [1]
で与えられることを示す.
の時間発展が,
マスター方程式 (master equation) とよばれる次の微分方程式 [1]
で与えられることを示す.
マスター方程式
(1)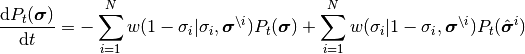
| [1] | 状態 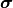 が が 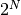 ( (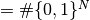 )
個あることを思い出せば, これは )
個あることを思い出せば, これは 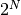 次元常微分方程式と考えても良い. 次元常微分方程式と考えても良い. |
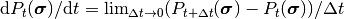 を,
時間
を,
時間 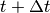 の確率をつなぐ関係式
の確率をつなぐ関係式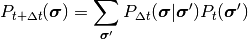
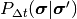 は時間
は時間 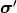 から
から 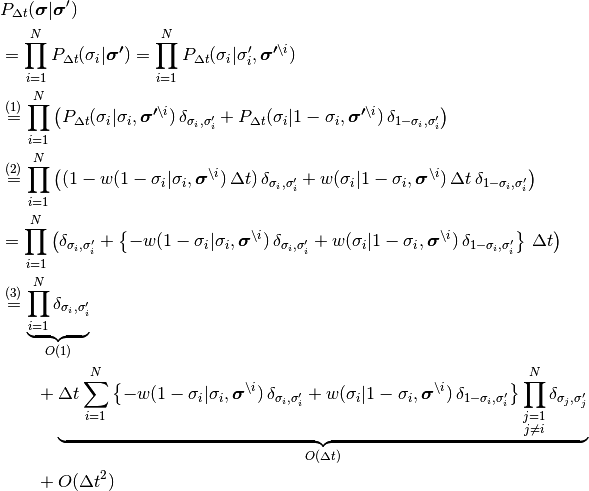
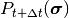 を評価する:
を評価する: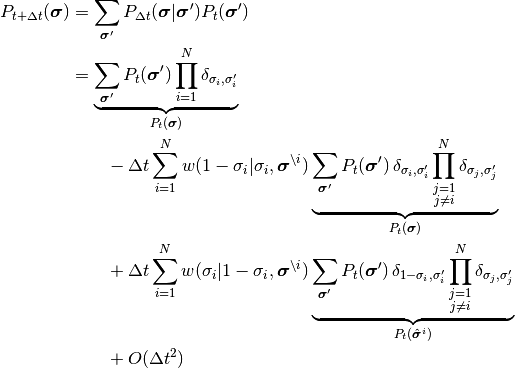
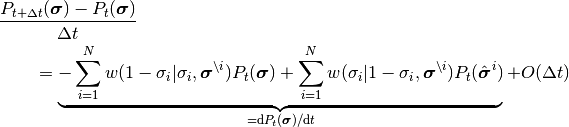
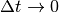 で消えない第1項と第2項は確かに式
で消えない第1項と第2項は確かに式