確率変数の収束¶
大数の法則 (law of large numbers)¶
課題
LNN について書く
大数の法則 (law of large numbers)
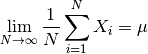
無相関変数に対する大数の法則¶
大数の法則が成り立つためには確率変数が同一の分布の従う条件や, 独立であるという条件は実は必要ではない. 確率変数の分散に「有界性」があり, (独立ではなく) 無相関であれば十分である. 本稿では, 以下の定理 ([Cinlar2011] の Proposition III.6.13 (p.121) より) を繰り返し用いる.
無相関変数に対する大数の法則
確率変数 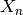 (
(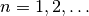 ) が無相関で,
ある非ゼロで正の増加列
) が無相関で,
ある非ゼロで正の増加列 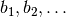 を用いて
を用いて
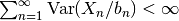 とできるならば,
とできるならば, 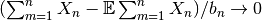 が
が 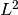 収束と確率収束の意味で成り立つ.
収束と確率収束の意味で成り立つ.
本稿では確率変数の収束の細かい違いについて神経質に使い分けないが,
前者は
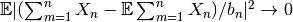 ,
後者は
,
後者は
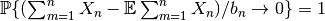 を意味する.
を意味する.
中心極限定理 (central limit theorem)¶
課題
CLT について書く
自己平均性 (self-averaging property)¶
確率変数 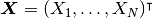 がすべての
がすべての
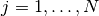 について
について
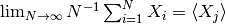 を満たす時, 確率変数
を満たす時, 確率変数 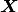 は自己平均的である
(
は自己平均的である
(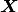 is self-averaging) と呼ばれる.
ただし,
is self-averaging) と呼ばれる.
ただし, 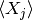 は 確率変数
は 確率変数 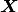 についての平均で, “average over realisations” や “average over samples”
と呼ばれる.
についての平均で, “average over realisations” や “average over samples”
と呼ばれる.
確率変数 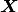 は例えばネットワークの状態
は例えばネットワークの状態
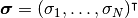 (モデルの定義 参照) である. この場合,
各
(モデルの定義 参照) である. この場合,
各 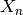 は有界なので,
は有界なので, 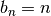 で 無相関変数に対する大数の法則
の「有界性」の条件
で 無相関変数に対する大数の法則
の「有界性」の条件
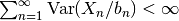 を満たす. さらに, すべての確率変数の平均が同一
を満たす. さらに, すべての確率変数の平均が同一 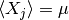 (
(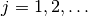 )
ならば, この定理より,
)
ならば, この定理より,
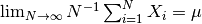 が言える.
が言える.