\(\newcommand{\D}{\text{d}} \newcommand{\I}{\text{i}} \newcommand{\E}{\text{e}} \newcommand{\Prob}{\mathbb{P}} \newcommand{\Expect}{\mathbb{E}} \newcommand{\Var}{\text{Var}} \newcommand{\PAvg}[1]{\left[#1\right]} \newcommand{\Avg}[1]{\left\langle#1\right\rangle} \newcommand{\AvgJ}[1]{\Avg{#1}_{\bm J}} \newcommand{\AvgDyn}[1]{\Avg{#1}_{\text{dyn.}}} \newcommand{\CAvg}[2]{\Avg{#1}_{\left|#2\right.}} \newcommand{\Devi}{\mathfrak{d}}\)
期待値の時間発展
参考
- [Ginzburg1994]
- この章の議論は, Ginzburg & Sompolinsky (1994) の Appendix A
に基づいている.
期待値の時間発展
マスター方程式 と同じ設定の下, ニューロン 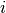 の状態の期待値
の状態の期待値 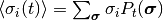 は次の方程式に従う.
は次の方程式に従う.
ただし, 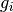 は状態
は状態 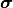 に基づき遷移確率を与える関数で,
に基づき遷移確率を与える関数で,
と定義される. つまり, 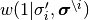 が
が 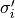 に依らない場合にのみ上式は成り立つ.
に依らない場合にのみ上式は成り立つ.
一般の場合の期待値の時間発展
期待値
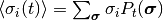 の時間微分をとると,
の時間微分をとると,
相関関数
課題
相関関数の従う方程式 (“two-time” second moment の時間発展) を導出する.
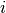 の状態の期待値
の状態の期待値 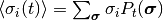 は次の方程式に従う.
は次の方程式に従う.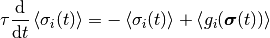
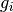 は状態
は状態 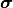 に基づき遷移確率を与える関数で,
に基づき遷移確率を与える関数で,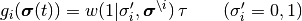
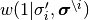 が
が 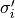 に依らない場合にのみ上式は成り立つ.
に依らない場合にのみ上式は成り立つ.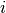 の状態の期待値
の状態の期待値 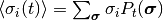 は次の方程式に従う.
は次の方程式に従う.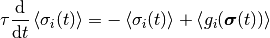
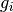 は状態
は状態 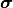 に基づき遷移確率を与える関数で,
に基づき遷移確率を与える関数で,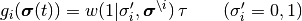
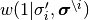 が
が 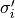 に依らない場合にのみ上式は成り立つ.
に依らない場合にのみ上式は成り立つ.