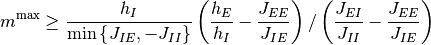均衡条件不等式¶
ここでは, はじめての興奮・抑制均衡 と 強フィードバック系 の解析を興奮・抑制ネットワークが外部からの興奮性入力を受ける系にあてはめ, このネットワークは「発火率がゼロの固定点は持たない」という条件から, 均衡条件不等式 (2) を導く. さらに, 「発火率が飽和するような固定点を持たない」という仮定を加えれば不等式 (4), (6) などの条件も導くことが出来るが, これらは単純な条件では無いことと, 外部入力が十分弱ければつねに成立することから, ニューラルネットワークの研究ではこれらの条件は通常は無視されている. また, 「発火率が発散しない」という条件から, 不等式 (5) も導くことが出来, 原著 [vanVreeswijk1998] ではこれも含めて均衡条件不等式と呼んでいる. 無活動・均衡-固定点の非存在条件 で 均衡条件不等式 (2) を導くまでが重要で, それ以降の議論は読まなくても他の章の内容は理解できる.
強フィードバック系 の解析と同様, 強フィードバック極限
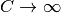 を考え, すべての漸近関係はすべてこの極限についてのものとするので “(as
を考え, すべての漸近関係はすべてこの極限についてのものとするので “(as 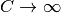 )” は省略する.
)” は省略する.
興奮・抑制ネットワーク¶
強フィードバック系 で扱った力学系が二次元 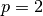 で,
系の状態
で,
系の状態 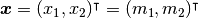 の第1, 第2成分はそれぞ興奮性と抑制性の集団の発火率を表すとする.
つまり, つねに
の第1, 第2成分はそれぞ興奮性と抑制性の集団の発火率を表すとする.
つまり, つねに 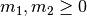 である.
また, ベクトルや行列の添字は 1, 2 の代わりに
である.
また, ベクトルや行列の添字は 1, 2 の代わりに 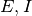 を適宜使い,
例えば
を適宜使い,
例えば 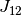 と
と 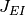 は同義である.
強フィードバック系 と同様, 系への「全入力」を
は同義である.
強フィードバック系 と同様, 系への「全入力」を
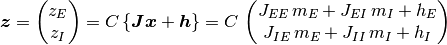
で定義する.
関数 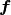 は, いわゆる入出力関係 (input-output relationship;
transfer function) を表すので,
は, いわゆる入出力関係 (input-output relationship;
transfer function) を表すので, 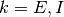 についてどんな入力
についてどんな入力 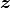 についても
についても 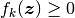 であり,
さらに
であり,
さらに 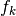 は強い興奮性の入力 (
は強い興奮性の入力 (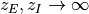 )
で飽和し, 強い抑制性の入力 (
)
で飽和し, 強い抑制性の入力 (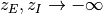 ) で出力が無くなる, という条件を追加する. 形式的に書くと
) で出力が無くなる, という条件を追加する. 形式的に書くと
(1)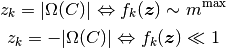
となる. ここで, 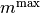 はフィードバック強度
はフィードバック強度 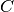 に依存しない正の定数で, 両集団の発火率の上限を与える.
定数
に依存しない正の定数で, 両集団の発火率の上限を与える.
定数 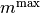 は集団ごとに違う値を考えても良いが,
は集団ごとに違う値を考えても良いが, 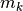 と
と 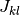 をスケールすれば同じ値にすることができるので,
この仮定は一般性を損なわない. さらに, 発火率の上限が存在しない場合
(
をスケールすれば同じ値にすることができるので,
この仮定は一般性を損なわない. さらに, 発火率の上限が存在しない場合
(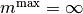 ) でも, 以下の議論は成り立つ. [1]
) でも, 以下の議論は成り立つ. [1]
| [1] | 片方の集団の発火率の上限が存在し, もう片方の発火率の上限が存在しない場合は扱っていないが, そんな変なモデルを考える必要は無いだろう. |
興奮性の集団と抑制性のふたつの集団が興奮性の外部入力を受ける系について解析するので, パラメタには
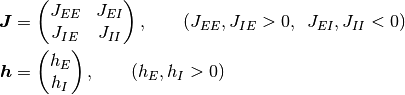
なる制限がかかる.
興奮・抑制ネットワークの均衡固定点¶
均衡固定点の線型性 より, 均衡固定点は
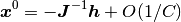
を満たすことが分かった. これは単なる二次の線型方程式なので, 均衡固定点は形式的に
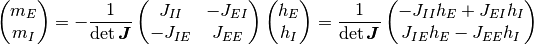
と書ける. これ以降の数式では固定点を表す上付き添字 0 は省略する.
この均衡固定点以外に, 非均衡固定点が存在する可能性がある. 定性的に場合分けをすると, 次の5つの場合が想定できる.
| 固定点 | 定義 |
|---|---|
| 無活動-固定点 | 両方の集団の発火率がゼロ |
| 無活動・均衡-固定点 | 片方の集団の発火率がゼロで, もう片方の集団の発火率がゼロでもなく飽和もしていない |
| 飽和-固定点 | 両方の集団の発火率が飽和している |
| 飽和・均衡-固定点 | 片方の集団の発火率が飽和していて, もう片方の集団の発火率がゼロでもなく飽和もしていない |
| 飽和・無活動-固定点 | 片方の集団の発火率が飽和していて, もう片方の集団の発火率がゼロ |
ただし, 発火率の上限が無い (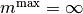 ) 場合, ここでの「飽和」は発火率の発散を意味する.
) 場合, ここでの「飽和」は発火率の発散を意味する.
無活動-固定点 は, 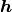 の成分が正である限り存在できない.
これは,
の成分が正である限り存在できない.
これは, 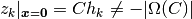 より, 自明である.
より, 自明である.
条件: 均衡固定点の発火率は非負¶
この均衡固定点が存在するためには 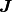 の行列式
の行列式
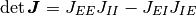
が非ゼロであることが必要条件である. さらに, 発火率が非負であるという条件を考慮すると, 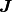 と
と 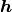 は
は
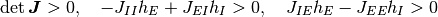
または, 上記の不等号をすべてひっくり返した
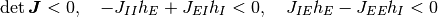
なる不等式系を満たす必要があることが分かる. これを変形すると,
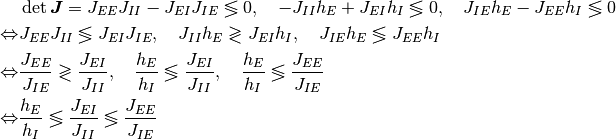
を得る.
(2)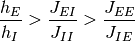
(3)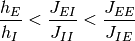
無活動・均衡-固定点の非存在条件¶
片方の集団の発火率がゼロで, もう片方の集団の発火率がゼロでもなく飽和もしていない, 無活動・均衡-固定点 存在しない(十分)条件を求める.
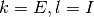 または
または 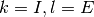 とする.
集団
とする.
集団 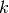 の発火率がゼロ (
の発火率がゼロ (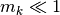 ) だとすると,
この状態が固定点となる必要十分条件は, 式 (1) より,
) だとすると,
この状態が固定点となる必要十分条件は, 式 (1) より,
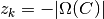 つまり,
つまり,
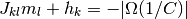
である. 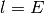 ならば左辺の項はすべて正なので実現不可能である. ゆえに,
ならば左辺の項はすべて正なので実現不可能である. ゆえに, 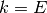 ,
, 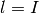 でなければならない.
さらに, 集団
でなければならない.
さらに, 集団 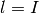 の発火率が非ゼロで有限
(
の発火率が非ゼロで有限
(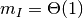 ) である必要十分条件は式 (1) より,
) である必要十分条件は式 (1) より,
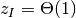 , つまり,
, つまり,
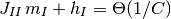
である. これを 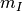 について解けば
について解けば
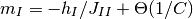
となる. これを 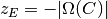 となる条件にあわせると,
となる条件にあわせると,
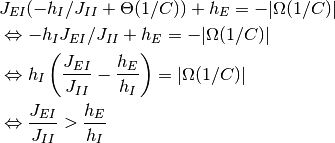
最後の式は, 式 (3) の必要条件であり, また, 式 (2) の下では偽である. ゆえに, 式 (2) はこの固定点が存在しない十分条件である. 以下では, すべて式 (2) が成り立つと仮定して議論を行う.
飽和-固定点の非存在条件¶
両方の集団の発火率が飽和した固定点 (飽和-固定点)
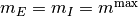 を考える.
条件 (1)
(
を考える.
条件 (1)
(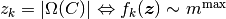 )
より,
)
より, 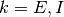 について,
について,
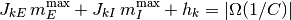
が成り立つことが, 飽和-固定点が存在する必要十分条件である.
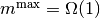 より, 左辺のオーダーは無条件に
より, 左辺のオーダーは無条件に 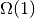 なので, これは条件
なので, これは条件
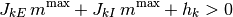
と同値である. これをさらに同値変形することにより,
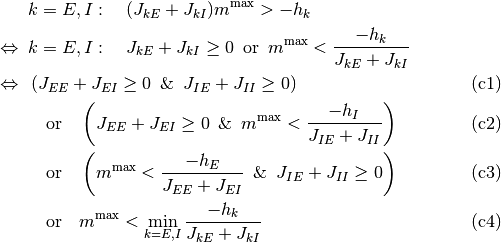
となる. 前節までで導いた均衡条件不等式 (2) は
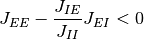
を導く. よって, 式 (2) の条件下で
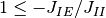 (つまり
(つまり 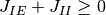 )
ならば
)
ならば 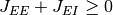 は満たされないことが分かる.
ゆえに, 式 (2) の条件下で
は満たされないことが分かる.
ゆえに, 式 (2) の条件下で
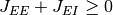 と
と 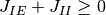 は同時に成立しない. ゆえに 式 (2) の条件下で外部入力に依存しない飽和-固定点の存在する条件 (c1) は成立し得ない.
以上の議論をあわせると, 式 (2) の条件下で
飽和-固定点 が存在しない必要十分条件は 条件 (c2)–(c3)
である. 条件 (c3) の否定をさらに強化した条件
は同時に成立しない. ゆえに 式 (2) の条件下で外部入力に依存しない飽和-固定点の存在する条件 (c1) は成立し得ない.
以上の議論をあわせると, 式 (2) の条件下で
飽和-固定点 が存在しない必要十分条件は 条件 (c2)–(c3)
である. 条件 (c3) の否定をさらに強化した条件
(4)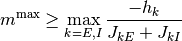
は, 条件 (c2)–(c3) の否定を導くので, 飽和-固定点 が存在しない, 十分条件である (単なる条件 (c3) の否定は, 上式において max ではなく min を使うことに注意). これから,
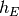 と
と 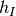 が十分小さければ, 飽和-固定点 は存在しないことが分かる.
が十分小さければ, 飽和-固定点 は存在しないことが分かる.
発火率が発散しない条件¶
発火率の上限が無い (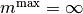 ) 場合, 条件 (c2)-(c3) は成立しようが無いから, (c1) が存在しなければ 飽和-固定点 (この場合は発火率が発散するような解) は存在しない.
さらに, 式 (2) の条件下で
) 場合, 条件 (c2)-(c3) は成立しようが無いから, (c1) が存在しなければ 飽和-固定点 (この場合は発火率が発散するような解) は存在しない.
さらに, 式 (2) の条件下で
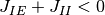 は
は
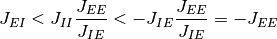
つまり 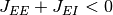 を導く
(
を導く
(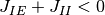 のほうが
のほうが 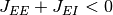 より厳しい条件). よって, 飽和-固定点 が存在しない,
必要十分条件は
より厳しい条件). よって, 飽和-固定点 が存在しない,
必要十分条件は
(5)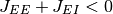
である. [2]
| [2] | [vanVreeswijk1998] の式 (4.10) の条件 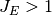 は は
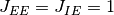 , , 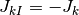 なる正規化(変数変換)の元で
なる正規化(変数変換)の元で 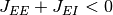 と同値である. 発火率の上限が無い場合はこの条件のみで
飽和-固定点 が存在しないことが保証されるが, 発火率の上限が有限の場合は, 条件 (c4) はまだ成立し得るので, 式 (4.10) だけでは飽和-固定点の存在を否定していない. と同値である. 発火率の上限が無い場合はこの条件のみで
飽和-固定点 が存在しないことが保証されるが, 発火率の上限が有限の場合は, 条件 (c4) はまだ成立し得るので, 式 (4.10) だけでは飽和-固定点の存在を否定していない. |
飽和・均衡-固定点の非存在条件¶
飽和・均衡-固定点 が存在しない十分条件を求める.
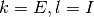 または
または 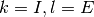 とする.
とする.
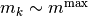 かつ集団
かつ集団 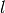 の発火率が非ゼロで飽和していない
(
の発火率が非ゼロで飽和していない
(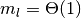 ) という必要十分条件は,
) という必要十分条件は,
 かつ
かつ 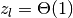 , つまり,
, つまり,
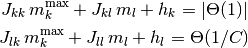
と同値である. 前者の式に後者の式を 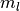 について解いた結果
について解いた結果
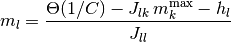
を代入して同値変形すると,
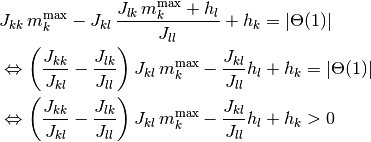
を得る. これを2つの場合に分けてさらに同値変形する.
飽和・無活動-固定点の非存在条件¶
飽和・無活動-固定点 は,
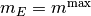 ,
, 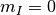 の場合は
の場合は
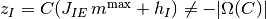 より存在できない.
一方,
より存在できない.
一方, 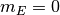 ,
, 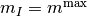 は
は
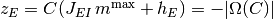 かつ
かつ
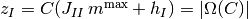 ,
つまり
,
つまり
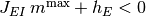 かつ
かつ
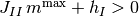 ならば存在する. これは,
ならば存在する. これは,
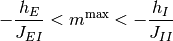
とも書ける. これが成立する必要条件は
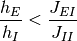
だが, これは式 (2) の下では成立しない. ゆえに, いかなる 飽和・無活動-固定点 も式 (2) の下では無条件で存在しない.
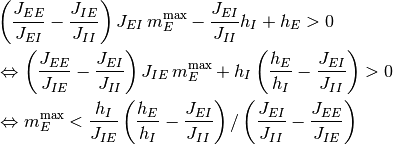
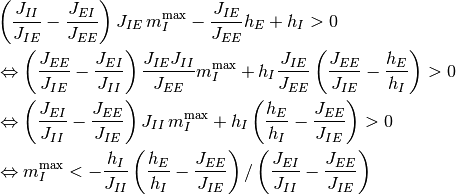
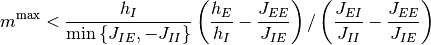
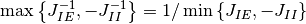 なる関係を用いた.
よって, いかなる
なる関係を用いた.
よって, いかなる