強フィードバック系¶
次の 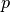 次元力学系を考えよう.
次元力学系を考えよう.
(1)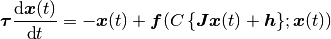
ここで,
 は時定数を決める行列,
は時定数を決める行列,
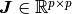 は系の状態
は系の状態 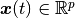 の各成分の相互作用を表す行列,
ベクトル
の各成分の相互作用を表す行列,
ベクトル 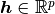 はこの系への外部入力を表す.
正数
はこの系への外部入力を表す.
正数 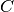 はこの系のフィードバックの強さを決めるパラメタである.
関数
はこの系のフィードバックの強さを決めるパラメタである.
関数 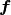 の第一引数
の第一引数 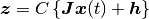 を系への「全入力」と呼ぶことにする. 上述の記号, 特にパラメタ
を系への「全入力」と呼ぶことにする. 上述の記号, 特にパラメタ
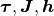 は
は 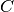 に依存しない.
フィードバック強度
に依存しない.
フィードバック強度 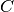 への依存性は全入力
への依存性は全入力 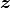 を経由する影響のみである.
本稿では, 極限
を経由する影響のみである.
本稿では, 極限 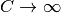 におけるこの系の振る舞いについて興味がある場合に, 式 (1) のような系を 強フィードバック系
(strong feedback system) と呼ぶ.
におけるこの系の振る舞いについて興味がある場合に, 式 (1) のような系を 強フィードバック系
(strong feedback system) と呼ぶ.
この節では, 強フィードバック系が均衡固定点と呼ばれる特別な固定点を持ち,
さらにその性質が系の詳細 (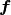 の定義) に依存しないことを示す.
均衡固定点のアイディア自体は簡単である (しかし, 今ここでアイディアにピンと来なくても以降の議論は読めるはずである).
ここでの「均衡」とは, 固定点
の定義) に依存しないことを示す.
均衡固定点のアイディア自体は簡単である (しかし, 今ここでアイディアにピンと来なくても以降の議論は読めるはずである).
ここでの「均衡」とは, 固定点 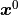 において,
フィードバック入力
において,
フィードバック入力 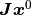 と 外部入力
と 外部入力 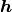 が打ち消し合って (= 均衡して), 「ほぼゼロ」になる, という意味である.
正しくは, これらが
が打ち消し合って (= 均衡して), 「ほぼゼロ」になる, という意味である.
正しくは, これらが 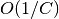 のオーダーで打ち消しあう,
つまり
のオーダーで打ち消しあう,
つまり 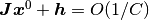 となることを言う.
これより
となることを言う.
これより 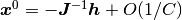 となるので,
まず固定点
となるので,
まず固定点 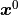 が外部入力について
が外部入力について 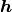 線型であるという性質が導かれる. さらに, 固定点
線型であるという性質が導かれる. さらに, 固定点 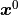 からの小さい摂動
からの小さい摂動 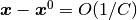 が, 大きな全入力の変化
が, 大きな全入力の変化 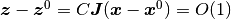 を生むので, 摂動への応答速度が速いだろうということも予想できる.
今, 均衡固定点が 存在すれば どのような性質を持つかを簡単に議論したが, この均衡固定点はいつも存在するのだろうか?
もちろん力学系に何らかの条件が必要だろうが, それは何だろうか?
また, 均衡固定点は他の種類の固定点に比べてどう特別なのだろうか?
を生むので, 摂動への応答速度が速いだろうということも予想できる.
今, 均衡固定点が 存在すれば どのような性質を持つかを簡単に議論したが, この均衡固定点はいつも存在するのだろうか?
もちろん力学系に何らかの条件が必要だろうが, それは何だろうか?
また, 均衡固定点は他の種類の固定点に比べてどう特別なのだろうか?
表記を簡潔にするために, 状態 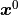 からの 「摂動」
からの 「摂動」
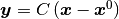 に対して
に対して 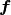 がどう変化するかを,
がどう変化するかを,
(2)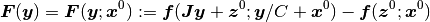
で定義する. 文脈から明らかな場合は, 第二引数は省略する.
正しく 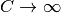 における系の振る舞いを表記するために,
における系の振る舞いを表記するために,
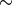 ,
, 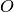 ,
, 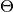 ,
, 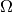 などの漸近関係記号を用いる (漸近解析 (Asymptotic analysis) を参照).
この節では, これらの記号はすべて
などの漸近関係記号を用いる (漸近解析 (Asymptotic analysis) を参照).
この節では, これらの記号はすべて 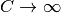 についての漸近関係を表すとする
(末尾の “as
についての漸近関係を表すとする
(末尾の “as 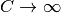 ” を省略する).
” を省略する).
関数 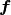 が満たすべき条件
が満たすべき条件
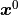 を力学系 (1) の任意の状態とし,
を力学系 (1) の任意の状態とし,
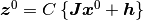 と定義する.
(この節では
と定義する.
(この節では 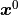 が固定点の場合しか考えないが, ここでの定義においては固定点でなくても良い.)
が固定点の場合しか考えないが, ここでの定義においては固定点でなくても良い.)
- 伝達性
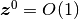 ならば
ならば
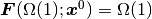 .
.省略せずに書けば, すべての
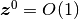 と
と
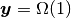 について,
について,(3)
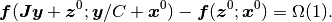
- 飽和性
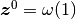 ならば
ならば
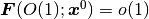 .
.省略せずに書けば, すべての
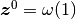 と
と
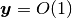 について,
について,(4)
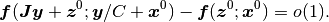
関数 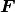 は陰に
は陰に 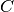 への依存性をもち,
状態
への依存性をもち,
状態 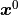 も
も 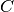 に依存しても良いことに注意.
に依存しても良いことに注意.
この関数 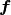 への条件は, 後述する均衡固定点の性質を導くための必要条件ではなく, さらに広いクラスでこれらの性質は成り立つ. しかし, この条件が応用上必要な力学系では成り立たないことは稀だろう. [1]
簡単のために 飽和性条件 の成り立たない力学系を扱うことも多いが,
この場合, 非均衡固定点は発散してしまい極限
への条件は, 後述する均衡固定点の性質を導くための必要条件ではなく, さらに広いクラスでこれらの性質は成り立つ. しかし, この条件が応用上必要な力学系では成り立たないことは稀だろう. [1]
簡単のために 飽和性条件 の成り立たない力学系を扱うことも多いが,
この場合, 非均衡固定点は発散してしまい極限 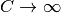 で存在しないのでその点まわりの振る舞いなどは議論する必要も無い.
非均衡固定点まわりでの振る舞い以外で 飽和性条件 は使わないので,
この条件は本質的な条件ではない. 結局, 伝達率条件 さえ成り立てば, 強フィードバック系の重要な性質はすべて保証される.
で存在しないのでその点まわりの振る舞いなどは議論する必要も無い.
非均衡固定点まわりでの振る舞い以外で 飽和性条件 は使わないので,
この条件は本質的な条件ではない. 結局, 伝達率条件 さえ成り立てば, 強フィードバック系の重要な性質はすべて保証される.
| [1] | これが成り立たない場合の取り扱いについては, 発火率モデル (rate model) の区分的線型関数についてのコメント参照. |
支配項均衡の方法による解析¶
力学系 (1) の固定点は
(5)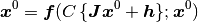
は満たす系の状態であり, それに対応する全入力を 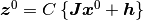 と置く.
全入力の各項がキャンセルしあって
と置く.
全入力の各項がキャンセルしあって 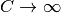 で発散しない場合, つまり
で発散しない場合, つまり 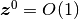 , あるいは同値の条件
, あるいは同値の条件
(6)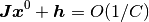
を満たす固定点を 均衡固定点 (balanced fixed point)
と呼ぶ. これが成り立たない場合, つまり固定点での全入力が発散して 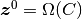 となる, あるいは同値の条件
となる, あるいは同値の条件
(7)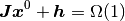
を満たす固定点を 非均衡固定点 (unbalanced fixed point) と呼ぶ. [2]
| [2] | ここでの均衡固定点や非均衡固定点に属さないクラスの固定点,
つまり 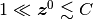 (同値だが別の表記では, (同値だが別の表記では,
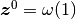 かつ かつ 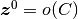 ) となる場合も考えられる. 例えば, ) となる場合も考えられる. 例えば, 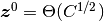 や や
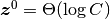 など. この場合, など. この場合,
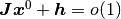 なので, 「広義の均衡固定点」と呼んでも良いかもしれない. しかし, 以下で導く小さい摂動に対する応答速度のオーダーに関する性質は, (狭義の) 均衡固定点のみに成り立つ. なので, 「広義の均衡固定点」と呼んでも良いかもしれない. しかし, 以下で導く小さい摂動に対する応答速度のオーダーに関する性質は, (狭義の) 均衡固定点のみに成り立つ. |
固定点まわりの座標系 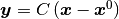 で微分方程式 (1) を書き直す. 座標変換
で微分方程式 (1) を書き直す. 座標変換 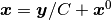 を施すと,
を施すと,
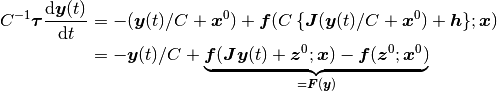
なので, これの両辺に 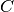 をかけて
をかけて
(8)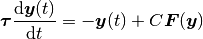
を得る (関数 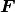 の定義については式 (2) を参照).
の定義については式 (2) を参照).
支配項均衡の方法 を使ってこの系の小さな摂動 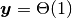 (元の座標系では
(元の座標系では 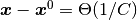 ) への応答を調べよう.
もし,
) への応答を調べよう.
もし, 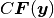 のオーダーが
のオーダーが 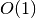 より大きい
(つまり
より大きい
(つまり 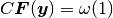 ) ならば,
) ならば,
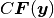 と
と 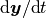 のオーダーが等しい (つまり,
のオーダーが等しい (つまり, 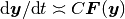 となる) ことが, 式 (8) の成り立つ必要条件である.
これは, 元の座標系では
となる) ことが, 式 (8) の成り立つ必要条件である.
これは, 元の座標系では 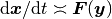 を意味する.
を意味する.
仮定 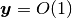 から,
から, 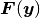 のオーダーは
のオーダーは
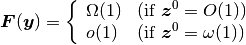
と見積もることが出来る.
ここで, 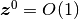 の場合は 伝達率条件 を,
の場合は 伝達率条件 を,
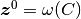 の場合は 飽和性条件 を用いた.
の場合は 飽和性条件 を用いた.
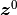 が素性の良い振る舞いをするなら (正確には
が素性の良い振る舞いをするなら (正確には
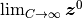 が有限値または無限大に収束すれば),
が有限値または無限大に収束すれば),
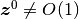 と
と 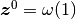 は同値なので,
は同値なので, 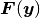 のオーダーはこのふたつしかありえない.
のオーダーはこのふたつしかありえない.
ゆえに, 小さな摂動 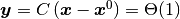 に関して,
均衡固定点 (
に関して,
均衡固定点 (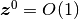 ) 周辺での応答速度のオーダーは
) 周辺での応答速度のオーダーは 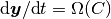 (
(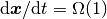 ) となり,
非均衡固定点など, それを満たさない固定点 (
) となり,
非均衡固定点など, それを満たさない固定点 (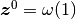 )
周辺での応答速度のオーダーは
)
周辺での応答速度のオーダーは 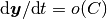 (
(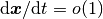 ) となる.
もし固定点
) となる.
もし固定点 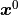 が安定ならば,
均衡固定点 (
が安定ならば,
均衡固定点 (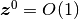 ) への収束は速く
(
) への収束は速く
(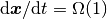 なので,
なので, 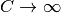 の極限で消えない),
非均衡固定点 (
の極限で消えない),
非均衡固定点 (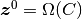 ) への収束は遅い
(
) への収束は遅い
(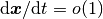 なので,
なので, 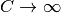 の極限で限りなく小さくなる)
ことが読み取れる.
以上の議論は抽象的な定義にのみ基づいているから, これは幅広いクラスの力学系の均衡固定点について成り立つ非常に強力な性質であるといえよう.
の極限で限りなく小さくなる)
ことが読み取れる.
以上の議論は抽象的な定義にのみ基づいているから, これは幅広いクラスの力学系の均衡固定点について成り立つ非常に強力な性質であるといえよう.
以上の議論では, 伝達率条件 と 飽和性条件 のみを仮定し, 固定点における 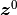 のオーダーについて (ほとんど相互排他的な) ふたつの場合にわけ, それぞれが固定点まわりの応答速度のオーダーが強フィードバック極限
のオーダーについて (ほとんど相互排他的な) ふたつの場合にわけ, それぞれが固定点まわりの応答速度のオーダーが強フィードバック極限 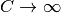 で消えない場合と限りなく小さくなる場合に対応することを示した. さらに, 応答速度が速い (
で消えない場合と限りなく小さくなる場合に対応することを示した. さらに, 応答速度が速い (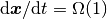 ) 場合が実は均衡固定点 (
) 場合が実は均衡固定点 (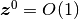 ) に対応することを示した.
つまり, 固定点まわりのダイナミクスについて漸近解析をすれば, 固定点は均衡固定点と均衡固定点でないものに自然と場合分けされるのである.
) に対応することを示した.
つまり, 固定点まわりのダイナミクスについて漸近解析をすれば, 固定点は均衡固定点と均衡固定点でないものに自然と場合分けされるのである.
均衡固定点の線型性¶
均衡固定点 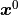 は, 式 (6) より,
は, 式 (6) より,
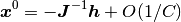
と書ける (ただし, 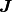 が可逆だと仮定した).
つまり, この固定点
が可逆だと仮定した).
つまり, この固定点 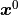 は外部入力
は外部入力 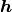 に対し,
に対し, 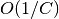 の誤差を除けば線型の関係を持つ. もしこの固定点が安定ならば, この系は外部入力に対し, 「線型な応答」をしていることになり, しかもそれが系の詳細を決める関数
の誤差を除けば線型の関係を持つ. もしこの固定点が安定ならば, この系は外部入力に対し, 「線型な応答」をしていることになり, しかもそれが系の詳細を決める関数 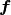 に依らないという著しい性質を持つ.
線型性から自明だが, 均衡固定点は存在すれば (極限
に依らないという著しい性質を持つ.
線型性から自明だが, 均衡固定点は存在すれば (極限 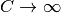 で) 一意である.
で) 一意である.
これが良く引用される「均衡固定点は線型性をもつ」という性質であるが,
この「線型性」は 厳密な意味での線型性 ではない. 固定点の満たすべき式 (5) を思い出せば, 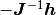 が
が
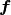 の 像 の 内部 にあるという条件が必要である.
神経科学での応用上
の 像 の 内部 にあるという条件が必要である.
神経科学での応用上 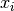 は常に発火率であるとみなされるから,
は常に発火率であるとみなされるから,
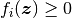 なので,
なので, 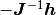 の成分に負の成分があってはならない. また,
の成分に負の成分があってはならない. また, 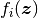 には上限がある (大きい入力については飽和する) ことが応用上自然だから,
結局, 均衡固定点の存在する
には上限がある (大きい入力については飽和する) ことが応用上自然だから,
結局, 均衡固定点の存在する 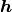 の領域は有界である.
つまり, 「均衡固定点は線型性をもつ」は間違いで,
「均衡固定点は閾値を超えてから飽和するまでは線型」が正しい.
の領域は有界である.
つまり, 「均衡固定点は線型性をもつ」は間違いで,
「均衡固定点は閾値を超えてから飽和するまでは線型」が正しい.
均衡固定点の安定性¶
支配項均衡の方法による解析 から, 均衡固定点まわりのダイナミクスは,
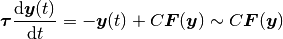
つまり,
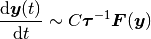
で記述されると分かる. よって, この系の安定性の解析は, 行列
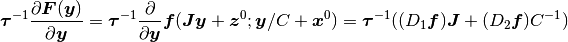
の固有値で決まる (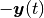 の寄与が消えていることに注意).
ただし,
の寄与が消えていることに注意).
ただし,
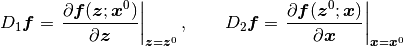
である. もし 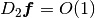 なら第二引数からの寄与が消え,
なら第二引数からの寄与が消え,
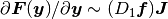 となる. これは, この方向への摂動が
となる. これは, この方向への摂動が 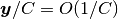 と小さいためである.
と小さいためである.
強フィードバック系の例¶
発火率モデル (rate model)¶
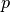 個の集団からなる発火率モデルのネットワークで, すべての集団の入出力関係 (input-output relationship あるいは transfer function)
がシグモイド関数
個の集団からなる発火率モデルのネットワークで, すべての集団の入出力関係 (input-output relationship あるいは transfer function)
がシグモイド関数 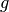 (例えば, ロジスティック関数
(例えば, ロジスティック関数
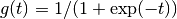 ) [3] で与えられているとすれば,
関数
) [3] で与えられているとすれば,
関数 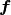 の
の 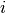 番目 (
番目 (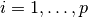 ) の成分は
) の成分は
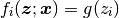
と書ける.
| [3] | 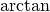 , ,  , Q関数 (の , Q関数 (の  軸を反転したもの) などでも構わない. 軸を反転したもの) などでも構わない. |
シグモイド関数 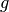 は
は 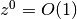 からの非ゼロの変化に対して,
必ず非ゼロの変化をうむ, つまり
からの非ゼロの変化に対して,
必ず非ゼロの変化をうむ, つまり
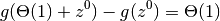
が成り立つ. これは 伝達率条件 の十分条件である.
また, ロジスティック関数の場合は極限 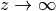 で
で 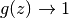 ,
極限
,
極限 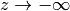 で
で 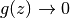 だから,
飽和性条件 も成り立つ.
一般に, シグモイド関数のように入出力関係が極限
だから,
飽和性条件 も成り立つ.
一般に, シグモイド関数のように入出力関係が極限 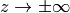 で有限の値に収束すれば 飽和性条件 は成り立つ.
有限の値に収束しなくても 飽和性条件 が成り立つ (かなり人工的な)
例として,
で有限の値に収束すれば 飽和性条件 は成り立つ.
有限の値に収束しなくても 飽和性条件 が成り立つ (かなり人工的な)
例として, 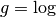 がある.
がある.
もし, 関数 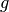 が
が
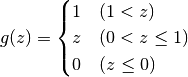
のような区分的線型関数の場合は, 伝達率条件 が成り立たない.
例えば, 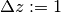 ,
, 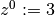 とおくと
とおくと 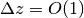 ,
, 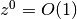 だが,
だが,
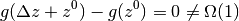
である. この場合, 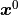 が均衡固定点であるためには,
各
が均衡固定点であるためには,
各 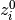 について,
について, 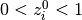 なる条件が必要である.
なる条件が必要である.
二状態ニューロンから成るネットワーク¶
二状態ニューロンから成るネットワーク
の平均場方程式も強フィードバック系である (平均場方程式の導出 を参照).
この場合は, 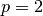 個の集団からなる力学系で, 状態は集団平均発火率
個の集団からなる力学系で, 状態は集団平均発火率 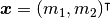 で,
外部入力は
で,
外部入力は 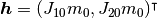 である. 関数
である. 関数 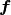 は,
は,
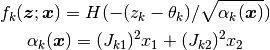
で定義される. また, フィードバックの強さは 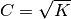 で決まる.
上記のシグモイド関数の場合と同様に, 伝達率条件 と
飽和性条件 が成り立つ.
で決まる.
上記のシグモイド関数の場合と同様に, 伝達率条件 と
飽和性条件 が成り立つ.