安定化可能性¶
均衡条件不等式 で求めた興奮・抑制ネットワークの均衡固定点の安定性を解析する. 均衡固定点の安定性 で示したように, 均衡固定点からのずれ 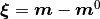 のダイナミクスは
のダイナミクスは
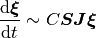
に従う. ただし,
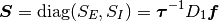
である. 均衡固定点の安定性を調べるためには行列 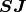 の固有値の実部を調べれば良い. 行列
の固有値の実部を調べれば良い. 行列 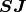 は
は
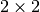 行列なので, その固有値は
行列なので, その固有値は
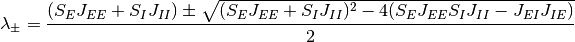
となる.
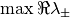 の負の成分は
の負の成分は
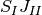 であるので,
であるので, 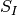 の大きい極限
の大きい極限 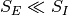 で
で 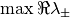 が負に出来なければ, この系が安定となる可能性は無い.
これは, 例えば
が負に出来なければ, この系が安定となる可能性は無い.
これは, 例えば 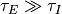 なる場合を考えることと同様である. この極限をとるためには
なる場合を考えることと同様である. この極限をとるためには 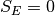 とすれば良い.
とすれば良い.
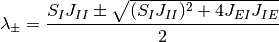
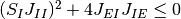 なら,
なら,
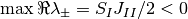 である.
である.
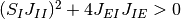 なら,
なら,
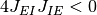 より,
より,
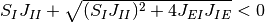 なので
なので 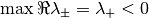 である.
ゆえに, 興奮・抑制ネットワークではどんな入出力関係
である.
ゆえに, 興奮・抑制ネットワークではどんな入出力関係 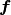 や結合パラメタ
や結合パラメタ 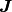 や外部入力
や外部入力 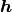 に対しても,
抑制性集団が興奮性集団に比べて十分速い時定数をもてば, 均衡固定点を漸近安定に出来る.
に対しても,
抑制性集団が興奮性集団に比べて十分速い時定数をもてば, 均衡固定点を漸近安定に出来る.