モデルの定義¶
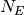 個の興奮性のニューロンと
個の興奮性のニューロンと
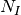 個の抑制性のニューロンが相互に結合したネットワークの特性を
個の抑制性のニューロンが相互に結合したネットワークの特性を
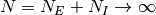 の極限で調べる. ここで, 興奮性ニューロンと抑制性ニューロンの非
の極限で調べる. ここで, 興奮性ニューロンと抑制性ニューロンの非
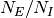 は
は 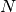 に依らない数に固定されているとする.
これらのニューロンは平均
に依らない数に固定されているとする.
これらのニューロンは平均 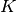 個のニューロンとランダムに結合され, その確率分布は
個のニューロンとランダムに結合され, その確率分布は
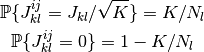
で定義される. [1]
| [1] | 原著 [vanVreeswijk1998] には確率は 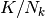 と書いてあるがこれは間違い.
と書いてあるがこれは間違い. |
それぞれのニューロンの状態は 0 か 1 の二値変数で表現され,
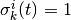 (
(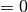 ) は活動 (無活動) 状態に対応する. ニューロンの状態は「バラバラ」なタイミング (後述) で更新され, そのニューロンへの入力
) は活動 (無活動) 状態に対応する. ニューロンの状態は「バラバラ」なタイミング (後述) で更新され, そのニューロンへの入力 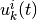 に依って, 状態は
に依って, 状態は
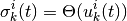
に更新される. ただし, 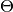 は
は
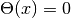 (
(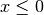 ),
),
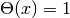 (
(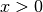 )
で定義される ヘヴィサイド関数 である. ニューロンへの入力は
)
で定義される ヘヴィサイド関数 である. ニューロンへの入力は
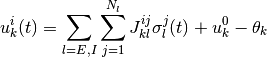
で定義される. 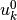 は外部入力を表し,
は外部入力を表し,
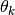 はニューロンの閾値を表す.
はニューロンの閾値を表す. 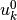 が外部集団からの入力を表すならば, その大きさは
が外部集団からの入力を表すならば, その大きさは 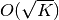 のオーダーになるはずである (はじめに 参照).
よって,
のオーダーになるはずである (はじめに 参照).
よって, 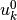 は外部集団との結合強度
は外部集団との結合強度 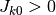 と外部集団の「活動率」
と外部集団の「活動率」 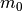 を使い,
を使い,
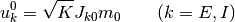
と置く.
集団 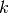 のニューロン
のニューロン 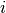 はそれぞれ平均
はそれぞれ平均 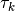 の時間間隔で「バラバラ」に (非同期的に) 更新される. ここでは,
各ニューロンの 更新の時間間隔は平均
の時間間隔で「バラバラ」に (非同期的に) 更新される. ここでは,
各ニューロンの 更新の時間間隔は平均 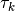 の独立な指数分布に従う (つまり, 各ニューロンの更新は独立なポアソン過程である) とする. [2]
の独立な指数分布に従う (つまり, 各ニューロンの更新は独立なポアソン過程である) とする. [2]
| [2] | 更新のタイミングがランダムでないバージョンのネットワークも [vanVreeswijk1998] では解析していて, その統計的な振る舞いは同一であることが示されている. |