平均場方程式の導出¶
ニューロン 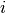 の初期値
の初期値 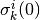 とその更新のランダム性と初期値
とその更新のランダム性と初期値 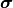 に 関する平均を
に 関する平均を 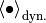 [1] と書き,
ニューロン
[1] と書き,
ニューロン 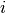 の(局所)活動率を
の(局所)活動率を
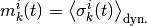
と定義する.
| [1] | 初期値 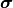 に関する平均とは, 時刻 0 での集団活動率 に関する平均とは, 時刻 0 での集団活動率
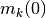 が が 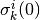 が 1 の確率で,
それぞれの が 1 の確率で,
それぞれの 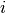 について について 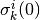 が独立, という確率分布に関する平均である. が独立, という確率分布に関する平均である. |
課題
他の場所では, 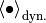 は使われていない. 使うべき?
例えば, 他の場所では
は使われていない. 使うべき?
例えば, 他の場所では 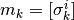 だけど, ここでは
だけど, ここでは
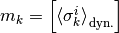 である.
である.
ニューロン 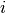 への入力が閾値を超える確率 [2] は, 更新時間のランダム性に関する平均
への入力が閾値を超える確率 [2] は, 更新時間のランダム性に関する平均 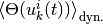 で表すことが出来る.
[3] さらに, 更新のタイミングはポアソン過程で表され, 入力が閾値を超えていた場合に状態 1 へ遷移する単位時間当たりの条件付き確率は,
で表すことが出来る.
[3] さらに, 更新のタイミングはポアソン過程で表され, 入力が閾値を超えていた場合に状態 1 へ遷移する単位時間当たりの条件付き確率は, 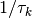 である. こられらを合わせると, 単位時間あたりにニューロン
である. こられらを合わせると, 単位時間あたりにニューロン 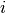 が状態を
1 に遷移する確率は
が状態を
1 に遷移する確率は 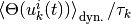 で与えられていることが分かる. 期待値の時間発展 の関係式を用いれば,
で与えられていることが分かる. 期待値の時間発展 の関係式を用いれば,
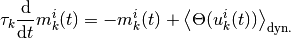
と書くことができる.
| [2] | 正確には, 系の状態 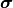 が与えられた時の条件付き確率, である. が与えられた時の条件付き確率, である. |
| [3] | 確率変数 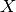 について事象 について事象 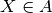 が起こる確率は指示関数 (indicator function) が起こる確率は指示関数 (indicator function) 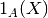 を用いて を用いて
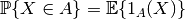 と書けることを思い出そう. と書けることを思い出そう. |
この式の集団平均をとる (つまり両辺に 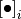 を施す) と,
集団活動率
を施す) と,
集団活動率 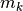 のダイナミクスを表す式
のダイナミクスを表す式
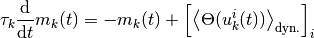
を得る. この節では, 右辺第二項
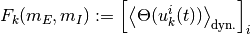
を計算する. 素朴に考えれば右辺は系の微視的な状態 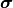 に依存しているはずだが, 左辺は巨視的な状態, つまり集団活動率
に依存しているはずだが, 左辺は巨視的な状態, つまり集団活動率 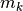 のみに依存することを主張している. この微視的な状態への非依存性は
のみに依存することを主張している. この微視的な状態への非依存性は 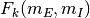 の計算の過程で自動的に出てくる結果である.
の計算の過程で自動的に出てくる結果である.
確率 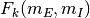 は以下の仮定 [4] のもとで計算することが出来る.
は以下の仮定 [4] のもとで計算することが出来る.
仮定
すべてのニューロンの活動が無相関である.
形式的に書けば,
いかなるふたつのニューロン 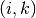 と
と 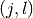 (
(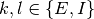 ,
, 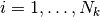 ,
,
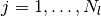 ) についても,
それぞれの活動
) についても,
それぞれの活動
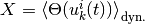 ,
,
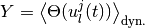 はすべての時間
はすべての時間 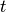 について無相関, つまり,
について無相関, つまり,
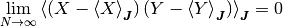
が, 成り立つ.
| [4] | 原著 [vanVreeswijk1998] での仮定は「すべてのニューロンについて, それに結合しているすべてのニューロンの活動が無相関である」であり, 本稿で使っている仮定より若干弱い. しかし, 無相関性の「証明」
より本稿で使っている仮定は [vanVreeswijk1998] の仮定と同じ条件
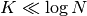 で成り立つことが分かる. さらに,
すべてのニューロンが無相関でなければ, 無相関変数に対する大数の法則 が使えない
(自己平均性 (self-averaging property) を参照). で成り立つことが分かる. さらに,
すべてのニューロンが無相関でなければ, 無相関変数に対する大数の法則 が使えない
(自己平均性 (self-averaging property) を参照). |
これは, 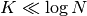 が成り立てば成り立つ.
詳しい議論については, 無相関性の「証明」 を参照.
が成り立てば成り立つ.
詳しい議論については, 無相関性の「証明」 を参照.
自己平均性 (self-averaging property) を ![[\Theta(u_k^i (t))]_i](../_images/math/30d9028d4a7446d37e92c7eb658addc642e51574.png) の計算に適用すれば,
の計算に適用すれば, ![[\bullet]_i](../_images/math/6c5e219bcc303b9b9ab0a6536cf4357e64c7c3ae.png) と
と 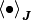 を交換することが出来て,
を交換することが出来て,
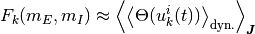
を計算すれば良いことが分かる.
ニューロン 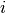 が
が
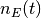 個の興奮性ニューロンと
個の興奮性ニューロンと
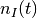 個の抑制性ニューロンから入力を受けているとすれば, その全入力は
個の抑制性ニューロンから入力を受けているとすれば, その全入力は
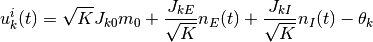
となる. 確率 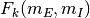 はこの入力が正である確率であり,
はこの入力が正である確率であり,
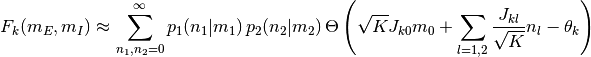
となる. ただし, 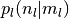 は集団
は集団
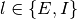 の活動率が
の活動率が 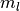 の時にニューロン
の時にニューロン 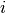 が集団
が集団 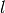 から
から 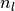 個の入力を受ける確率であり,
個の入力を受ける確率であり,
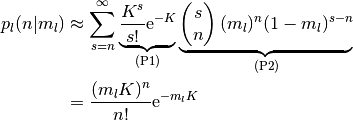
となる. ここで, (P1) は集団 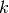 のニューロン (どのニューロンでも成立する)
が集団
のニューロン (どのニューロンでも成立する)
が集団 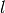 の
の  個のニューロンからの結合を持つ確率であり,
(P2) はその
個のニューロンからの結合を持つ確率であり,
(P2) はその  個のニューロンのうち
個のニューロンのうち 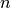 個のニューロンが活動している
(
個のニューロンが活動している
(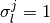 である) 確率である.
最後の等式は,
である) 確率である.
最後の等式は, 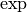 の定義に基づけば、以下の計算で確認できる.
の定義に基づけば、以下の計算で確認できる.
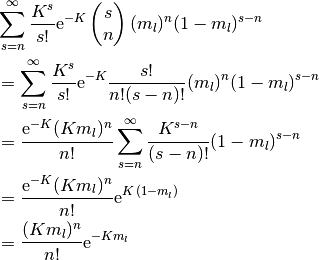
この確率分布は平均と分散が 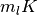 の ポアソン分布 (Poisson distribution) なので, 極限
の ポアソン分布 (Poisson distribution) なので, 極限 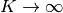 , つまりこの平均と分散が大きな極限では
ガウス分布 (Gaussian distribution)
, つまりこの平均と分散が大きな極限では
ガウス分布 (Gaussian distribution)
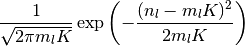
で近似できる. この極限 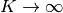 で,
で,
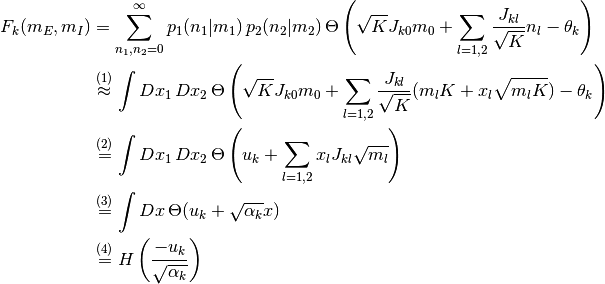
と計算できる. ここで,
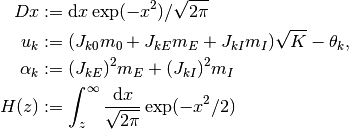
である. 上記の 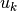 と
と 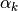 はただ変数に名前をつけただけだが, これらの物理的意味については 入力のゆらぎ を参照せよ.
はただ変数に名前をつけただけだが, これらの物理的意味については 入力のゆらぎ を参照せよ.
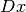 は ガウス測度 (Gaussian measure) と呼ばれるただの省略記号である.
関数
は ガウス測度 (Gaussian measure) と呼ばれるただの省略記号である.
関数 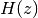 は Q関数 と呼ばれる関数である.
上の計算では,
(1)
は Q関数 と呼ばれる関数である.
上の計算では,
(1) 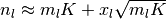 なる近似と
ガウス確率変数の変数変換,
(2)
なる近似と
ガウス確率変数の変数変換,
(2) 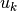 の定義,
(3) ヘヴィサイド関数の多重ガウス積分とQ関数 の関係,
(4)
の定義,
(3) ヘヴィサイド関数の多重ガウス積分とQ関数 の関係,
(4) 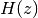 の定義をそれぞれ用いた.
の定義をそれぞれ用いた.
無相関性の「証明」¶
以下の議論は [Derrida1987] に依る.
今, 初期状態から 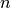 回の更新が起こったとする. いかなるニューロンも,
回の更新が起こったとする. いかなるニューロンも,
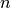 回の更新の前まで遡れば最大でも
回の更新の前まで遡れば最大でも 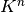 個 [5] のニューロンの初期状態に依存している.
2つのニューロンから伸びる「木」はそれぞれ平均で
個 [5] のニューロンの初期状態に依存している.
2つのニューロンから伸びる「木」はそれぞれ平均で 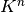 の「枝」をもつ.
この中で最低でも1つの枝が同じニューロンに繋がっている確率は,
(1) 2つの木からそれぞれの1つの枝を選ぶ方法の総数と,
(2) 1つのニューロンの選び方の総数と,
(3) ある1つのニューロンを2回選ぶ確率の積なので,
の「枝」をもつ.
この中で最低でも1つの枝が同じニューロンに繋がっている確率は,
(1) 2つの木からそれぞれの1つの枝を選ぶ方法の総数と,
(2) 1つのニューロンの選び方の総数と,
(3) ある1つのニューロンを2回選ぶ確率の積なので,
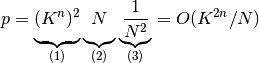
となる.
これが 0 に漸近する, つまり  (as
(as 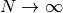 ) という条件から,
) という条件から,  が導かれる.
いかなる自然数
が導かれる.
いかなる自然数 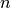 でもこれが成り立つには
でもこれが成り立つには
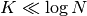 であれば十分である.
であれば十分である.
| [5] | ただし, 各ニューロンの結合の数が平均 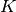 個のまわりでゆらいでいる効果は無視している. 個のまわりでゆらいでいる効果は無視している. |