入力のゆらぎ¶
ここでは, 入力のゆらぎ ![[(\Devi u_k^i (t))^2]_i](../_images/math/611f58ee5837aebbfec7822ef937ad72eafeb6bc.png) と集団平均活動率
と集団平均活動率 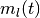 を結ぶ式
を結ぶ式
(1)![[(\Devi u_k^i (t))^2]_i
\xrightarrow{N \to \infty}
\sum_{l = E, I} ( J_{kl} )^2 \,
m_l(t)
=:
\alpha_k(t)](../_images/math/52e622466842bfe5a7e150135b24b44dda6c90fb.png)
を導出する. ここで ![[ \bullet ]_i](../_images/math/13fb29a53653bedc6f836c865b2b2a7d8ab9505b.png) は集団
は集団 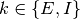 内のニューロンに関する
集団平均 (population average;
添字
内のニューロンに関する
集団平均 (population average;
添字 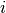 に沿った平均) を表し,
に沿った平均) を表し,
![[ \bullet ]_i = \frac{1}{N_k} \sum_{i=1}^{N_k} \bullet](../_images/math/7decae8e7d18553e902f9241eca67cb24a2e723c.png)
で定義される.
文脈からどの添字に関する平均かが明らかであれば, 添字 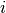 は省略する.
また,
は省略する.
また, 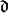 は集団平均からの偏差
は集団平均からの偏差 ![\Devi X_i := X_i - [X_i]_i](../_images/math/c3c5934f16c049f1ea4a226d38bd5ae7c1d52028.png) である.
である.
入力の集団平均¶
![u_k(t)
& =
[u_k^i (t)]_i
\\
& =
\left[
\sum_{l = E, I} \sum_{j=1}^{N_l} J_{kl}^{ij} \sigma_l^j(t)
+ u_k^0 - \theta_k
\right]_i
\\
& =
\sum_{l = E, I}
\underbrace{
\left[
\sum_{j=1}^{N_l} J_{kl}^{ij} \sigma_l^j(t)
\right]_i
}_{(*)}
+ u_k^0 - \theta_k](../_images/math/af0daec51112f842321f86eaae9982b35e318213.png)
この (*) は以下のように近似的できる.
![(*)
& \overset{(1)} \approx
\sum_{j=1}^{N_l}
\left[
J_{kl}^{ij}
\right]_i
\sigma_l^j(t)
\\
& \overset{(2)} \approx
\sum_{j=1}^{N_l}
J_{kl} \frac{\sqrt K}{N_l}
\sigma_l^j(t)
\\
& \overset{(3)} =
J_{kl} \frac{\sqrt K}{N_l}
\sum_{j=1}^{N_l}
\sigma_l^j(t)
\\
& \overset{(4)} =
J_{kl} \sqrt K
\left[
\sigma_l^j(t)
\right]_j
\\
& \overset{(5)} =
J_{kl} \sqrt K m_l(t)](../_images/math/d773310270a4b503dcd6211d865ac30d70eb2a9c.png)
ここで,
(1) は, ![[ \bullet ]_i](../_images/math/13fb29a53653bedc6f836c865b2b2a7d8ab9505b.png) の線型性 (よって和
の線型性 (よって和 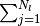 と集団平均
と集団平均 ![[ \bullet ]_i](../_images/math/13fb29a53653bedc6f836c865b2b2a7d8ab9505b.png) は演算順序を入れ替えて良い) と
は演算順序を入れ替えて良い) と 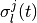 が
が 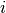 に依らないこと
(これの正しい解説は ニューロンの状態と結合係数の相関 を参照),
(2) 大数の法則 (law of large numbers) より算術平均は期待値に収束する, つまり
に依らないこと
(これの正しい解説は ニューロンの状態と結合係数の相関 を参照),
(2) 大数の法則 (law of large numbers) より算術平均は期待値に収束する, つまり 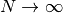 の極限で
の極限で ![\left[ J_{kl}^{ij} \right]_i \to \AvgJ{J_{kl}^{ij}}](../_images/math/2927c5063dfe1716f31985a63b2faa51187a2e69.png) が成り立つことと,
が成り立つことと, 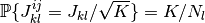 と
と 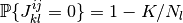 から期待値は
から期待値は 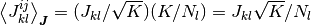 となること,
(3)
となること,
(3) 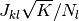 が
が 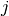 に依らない定数であること,
(4) 集団平均の定義,
(5)
に依らない定数であること,
(4) 集団平均の定義,
(5) 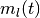 の定義を用いた.
の定義を用いた.
これらの計算を合わせ, 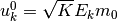 を思い出せば, 入力の集団平均
を思い出せば, 入力の集団平均 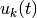 は
は
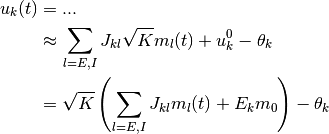
となる.
ニューロンの状態と結合係数の相関¶
上記の式変換(1)で「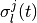 が
が 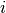 に依らない」ことを用いたが,
これは正しくは,
に依らない」ことを用いたが,
これは正しくは, 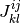 と
と 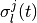 の相関が無い [1] と仮定することで,
の相関が無い [1] と仮定することで, 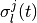 は
は 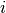 , つまり
, つまり 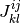 に依らずに決まるから集団平均
に依らずに決まるから集団平均 ![[ \bullet ]_i](../_images/math/13fb29a53653bedc6f836c865b2b2a7d8ab9505b.png) の演算にとっては定数として扱えることから言える. この
の演算にとっては定数として扱えることから言える. この 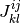 と
と 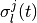 が無相関であるという仮定は,
が無相関であるという仮定は,
- 事象
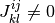 と
と 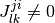 が独立
(
が独立
(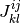 の定義より)
の定義より) 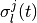 と
と 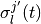 (
(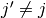 )
が無相関という仮定
)
が無相関という仮定
から正当化される.
この無相関の仮定は有限の 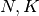 では正しくないので, この式変形は完全な等号では結ばれず,
では正しくないので, この式変形は完全な等号では結ばれず, 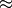 と書いている.
と書いている.
| [1] | 原著 [vanVreeswijk1998] では,
と説明されている. この “equation 3.11” はここで扱っている入力の集団平均 |
課題
式変形 ![[J_{kl}^{ij} \, \sigma_l^j(t)]_i
= [J_{kl}^{ij}]_i \, \sigma_l^j(t)](../_images/math/e392bb35ab90bcd84bc2b28b6696e34f73edccfe.png) を正当化する議論をもっと形式化する.
説明に自然言語つかいすぎ!
を正当化する議論をもっと形式化する.
説明に自然言語つかいすぎ!
先に確率平均に行く方法もあるかも?:
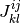 と
と 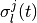 が独立だという近似のもと,
が独立だという近似のもと, ![[J_{kl}^{ij} \sigma_l^j(t)]_i
\approx \AvgJ{J_{kl}^{ij} \sigma_l^j(t)}
= \AvgJ{J_{kl}^{ij}} \AvgJ{\sigma_l^j(t)}](../_images/math/54201bf3c436e043c4762cac2a5c98130c525fd7.png) であることを用いる. この
であることを用いる. この 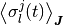 は式変形 (4) にあるように,
さらに集団平均
は式変形 (4) にあるように,
さらに集団平均 ![[\bullet]_j](../_images/math/9d059a0f82910b8e19277805ddc0ed821519e976.png) がかかるから,
がかかるから,
![\left[ \AvgJ{\sigma_l^j(t)} \right]_j = \AvgJ{[\sigma_l^j(t)]_j}
= \AvgJ{m_l(t)}](../_images/math/f5a31c4ce32b1114996c89b3da3f98d6a8a2accc.png) となる. この系は self-averaging なので (とどこかで説明する必要があるけど,)
となる. この系は self-averaging なので (とどこかで説明する必要があるけど,) 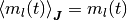 となる.
となる.
入力のゆらぎ¶
![&
[(\Devi u_k^i (t))^2]
\\
& \overset{(1)} =
\left[ \left( \Devi \left\{
\sum_{l = E, I} \sum_{j=1}^{N_l} J_{kl}^{ij} \sigma_l^j(t))
\right\} \right)^2 \right]_i
\\
& \overset{(2)} =
\left[ \left(
\sum_{l = E, I} \sum_{j=1}^{N_l} J_{kl}^{ij} \sigma_l^j(t))
\right)^2 \right]_i
-
\left[
\sum_{l = E, I} \sum_{j=1}^{N_l} J_{kl}^{ij} \sigma_l^j(t))
\right]_i^2
\\
& \overset{(3)} =
\left[ \left(
\sum_{l = E, I} \sum_{j=1}^{N_l} J_{kl}^{ij} \sigma_l^j(t))
\right)^2 \right]_i
-
K \left(\sum_{l = E, I} J_{kl} m_l(t) \right)^2](../_images/math/0e01acedc0a78c129273f3b35a8e43a0d244fa8f.png)
ここで,
(1)  ,
(2)
,
(2) ![[(\Devi x)^2] = [x^2] - [x]^2](../_images/math/fbc09ca49fb04e28055051285e8f51f5f8fdbcd3.png) ,
(3) 上記の
,
(3) 上記の 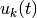 の計算 (特に (*) の部分)
を用いた.
の計算 (特に (*) の部分)
を用いた.
![&
\left[ \left(
\sum_{l = E, I} \sum_{j=1}^{N_l} J_{kl}^{ij} \sigma_l^j(t))
\right)^2 \right]_i
\\
& =
\left[
\sum_{l, l' = E, I} \sum_{j=1}^{N_l} \sum_{j'=1}^{N_{l'}}
J_{kl}^{ij} J_{kl'}^{ij'} \sigma_l^j(t)) \sigma_{l'}^{j'}(t))
\right]_i
\\
& =
\sum_{l, l' = E, I} \sum_{j=1}^{N_l} \sum_{j'=1}^{N_{l'}}
\underbrace{
\left[
J_{kl}^{ij} J_{kl'}^{ij'}
\right]_i
\sigma_l^j(t) \sigma_{l'}^{j'}(t)
}_{(*)}](../_images/math/b98d833cf3cdf1896e9a814ac658cbfb7adc69ec.png)
上式の (*) の和は, 恒等式
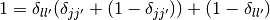 を用いて [2]
を用いて [2]
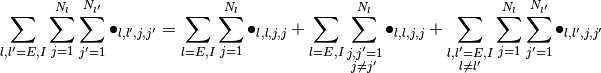
のように分解できる.
| [2] | 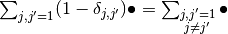 |
第一項の計算 (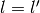 ,
, 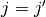 )¶
)¶
![&
\sum_{l = E, I} \sum_{j=1}^{N_l}
\left[
(J_{kl}^{ij})^2
\right]_i
(\sigma_l^j(t))^2
\\
& \overset{(1)} \approx
\sum_{l = E, I} \sum_{j=1}^{N_l}
\AvgJ{(J_{kl}^{ij})^2}
\, \sigma_l^j(t)
\\
& \overset{(2)} =
\sum_{l = E, I} \sum_{j=1}^{N_l}
\left( \frac{J_{kl}}{\sqrt K} \right)^2
\frac{K}{N_l}
\, \sigma_l^j(t)
\\
& =
\sum_{l = E, I} ( J_{kl} )^2
\frac{1}{N_l} \sum_{j=1}^{N_l} \sigma_l^j(t)
\\
& \overset{(3)} =
\sum_{l = E, I} ( J_{kl} )^2 \,
m_l(t)](../_images/math/5d13ec5c203f21e6826845fe9de47a3ef52e8fe1.png)
ここで,
(1) 大数の法則 (law of large numbers) と 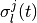 の取りうる値は 0 か 1 なので
の取りうる値は 0 か 1 なので 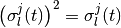 [3],
(2)
[3],
(2) 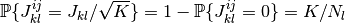 (結合確率の定義 を参照),
(3)
(結合確率の定義 を参照),
(3) ![m_l(t) = [\sigma_l^j(t)]_j = \sum_{j=1}^{N_l} \sigma_l^j(t) / N_l](../_images/math/f63ef28e1a48ba7f90c72f1d4f0b295317bd8c96.png) ,
を用いた.
,
を用いた.
| [3] | 二値変数のからむ計算ではよく使われるテクニック. |
第二項の計算 (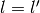 ,
, 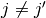 )¶
)¶
![&
\sum_{l = E, I} \sum_{\substack{j,j'=1 \\ j \neq j'}}^{N_l}
\left[
J_{kl}^{ij} J_{kl}^{ij'}
\right]_i
\, \sigma_l^j(t) \, \sigma_{l}^{j'}(t)
\\
& \overset{(1)} \approx
\sum_{l = E, I} \sum_{\substack{j,j'=1 \\ j \neq j'}}^{N_l}
\AvgJ{J_{kl}^{ij} J_{kl}^{ij'}}
\, \sigma_l^j(t) \, \sigma_{l}^{j'}(t)
\\
& \overset{(2)} =
\sum_{l = E, I} \sum_{\substack{j,j'=1 \\ j \neq j'}}^{N_l}
\left( \frac{J_{kl}}{\sqrt K} \right)^2
\frac{K}{N_l} \frac{K}{N_l}
\, \sigma_l^j(t) \, \sigma_{l}^{j'}(t)
\\
& =
K
\sum_{l = E, I} (J_{kl})^2
\frac{1}{N_l}
\sum_{j=1}^{N_l}
\sigma_l^j(t)
\left(
\sum_{j'=1}^{N_l}
\frac{1}{N_l}
\sigma_{l}^{j'}(t)
-
\frac{1}{N_l}
\sigma_{l}^{j}(t)
\right)
\\
& =
K
\sum_{l = E, I} (J_{kl})^2
\left(
\left\{
\frac{1}{N_l}
\sum_{j=1}^{N_l}
\sigma_l^j(t)
\right\}^2
-
\frac{1}{{N_l}^2}
\sum_{j=1}^{N_l}
(\sigma_{l}^{j}(t))^2
\right)
\\
& =
K
\sum_{l = E, I} (J_{kl})^2
\left(
(m_l(t))^2
-
\frac{1}{N_l}
m_l(t)
\right)](../_images/math/2d70849dff0f1555b2dfa8d8a5d3cb2f67d70db2.png)
ここで,
(1) 大数の法則 (law of large numbers),
(2) 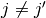 なので
なので 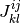 と
と 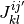 が独立であることと,
が独立であることと, 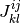 の確率分布
の確率分布
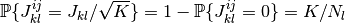 (結合確率の定義 を参照),
を用いた. 残りは単純な式変形である.
(結合確率の定義 を参照),
を用いた. 残りは単純な式変形である.
第三項の計算 (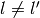 )¶
)¶
![&
\sum_{\substack{l, l' = E, I \\ l \neq l'}}
\sum_{j=1}^{N_l} \sum_{j'=1}^{N_{l'}}
\left[
J_{kl}^{ij} J_{kl'}^{ij'}
\right]_i
\, \sigma_l^j(t) \, \sigma_{l'}^{j'}(t)
\\
& \overset{(1)} \approx
\sum_{\substack{l, l' = E, I \\ l \neq l'}}
\sum_{j=1}^{N_l} \sum_{j'=1}^{N_{l'}}
\AvgJ{J_{kl}^{ij} J_{kl'}^{ij'}}
\, \sigma_l^j(t) \, \sigma_{l'}^{j'}(t)
\\
& \overset{(2)} =
\sum_{\substack{l, l' = E, I \\ l \neq l'}}
\sum_{j=1}^{N_l} \sum_{j'=1}^{N_{l'}}
\frac{J_{kl}}{\sqrt K} \frac{J_{kl'}}{\sqrt K}
\frac{K}{N_l} \frac{K}{N_{l'}}
\, \sigma_l^j(t) \, \sigma_{l'}^{j'}(t)
\\
& =
K
\sum_{\substack{l, l' = E, I \\ l \neq l'}}
J_{kl} J_{kl'}
\frac{1}{N_l} \sum_{j=1}^{N_l} \sigma_l^j(t)
\frac{1}{N_{l'}} \sum_{j'=1}^{N_{l'}} \sigma_{l'}^{j'}(t)
\\
& =
K
\sum_{\substack{l, l' = E, I \\ l \neq l'}}
J_{kl} J_{kl'} \, m_l(t) \, m_{l'}(t)](../_images/math/add958c2e000b3d9c3eeab42dfeaef4e8d5ab697.png)
ここで,
(1) 大数の法則 (law of large numbers),
(2) 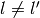 なので
なので 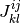 と
と 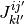 が独立であることと,
が独立であることと, 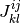 の確率分布
の確率分布
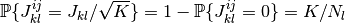 (結合確率の定義 を参照),
を用いた. 残りは単純な式変形である.
(結合確率の定義 を参照),
を用いた. 残りは単純な式変形である.
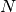 limit.
limit.![[(\Devi u_k^i (t))^2]_i
& =
\sum_{l = E, I} ( J_{kl} )^2 \,
m_l(t)
\\
& \qquad +
K
\sum_{l = E, I} (J_{kl})^2
\left(
(m_l(t))^2
-
\frac{1}{N_l}
m_l(t)
\right)
\\
& \qquad +
K
\sum_{\substack{l, l' = E, I \\ l \neq l'}}
J_{kl} J_{kl'} \, m_l(t) \, m_{l'}(t)
\\
& \qquad -
K \left(\sum_{l = E, I} J_{kl} m_l(t) \right)^2
\\
& =
\sum_{l = E, I} ( J_{kl} )^2 \,
m_l(t)
+
\frac{K}{N_l}
\sum_{l = E, I} (J_{kl})^2 m_l(t)
\\
& \qquad +
K
\underbrace{
\left(
\sum_{l, l' = E, I}
J_{kl} J_{kl'} \, m_l(t) \, m_{l'}(t)
-
\left(\sum_{l = E, I} J_{kl} m_l(t) \right)^2
\right)
}_{= 0}
\\
& =
\sum_{l = E, I} ( J_{kl} )^2 \,
m_l(t)
+
O(1/N)
\\
& \xrightarrow{N \to \infty}
\alpha_k(t)](../_images/math/26da931925e4cb4c02f7fdfd27f58acb98963b2c.png)